

The ideal (infinitely rigid) dome tweeter has a gradually increasing phase delta on-axis between tip and the rest of the driver. Actually, this is a distributed phenomenon, requiring an integration over the entire dome surface at every frequency since all points on the dome radiate with their own delay, so the actual dome shape will have a significant impact on the phase response from every point on the surface of the dome. The result is that there is a gradually increasing integrated phase delta with increasing frequency. It reaches a maximum, but not at the frequency where the wavelength is equal to twice the depth of the dome as might be expected. The maximum destructive interference is always where the phase delta = 1/2 wavelength. But this is not related to the total dome depth, meaning the distance from tip to surround attachment. Since it's a distributed phenomenon, it is probably somewhere part way between this distance, at a ring around the dome. It's not exactly half way because the shape of the dome determines this. Only an integration of the dome shape can determine this ring.
The demonstration of the tweeter response, both ideal and for two simulated non-ideal materials is in a paper by B&W on the their series 800 speaker system. I always thought this one to be a fascinating study.
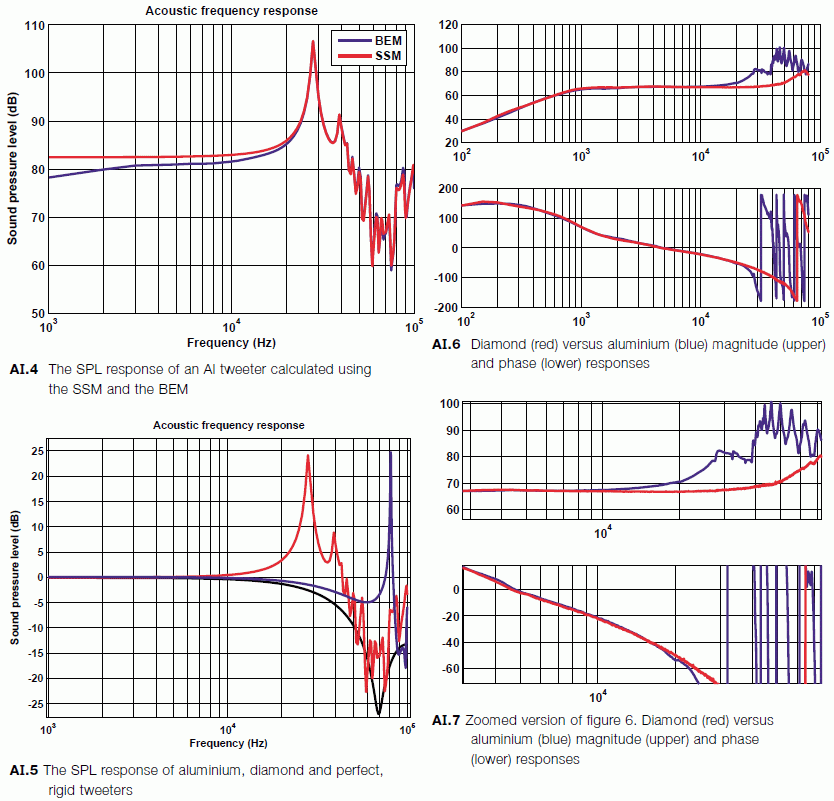
The key results from their modelling are in the set of graphs below. They modeled an ideal (infinitely rigid) dome, an aluminum one and a diamond one. They don't specify the dome shape. I suspect that is probably because there is no ideal shape, even for a theoretically infinitely rigid material. Change the shape and the interference pattern changes on-axis with likely a change to the minimum point, but also the off-axis changes as well, so the shape, as for real drivers, needs to take the off-axis into account as well as the on-axis. The shape and the material affect what they call "phase rolloff". This is due to the gradually changes integrated phase delta as frequency increases. Note that the driver breakup actually alters this significantly. They point out later that flat response is only attainable by utilizing breakup.
They analyzed two methods of modelling a dome, BEM and SSM. Below 1K there are significant differences that are explained in the paper. Above about 10K the two are essentially equivalent. Since they were only concerned with the high frequency aspect related to structural rigidity, they settled on SSM due it being much less computationally intensive.
Some interesting quotes from the paper:
The rigid response shows a characteristic roll off and deep null at approximately 70kHz caused by the interference effects owing to path length differences, commonly referred to as phase loss.
The response of the diamond tweeter is much closer to that of the perfect rigid tweeter below 20kHz than the aluminium tweeter. More specifically, at 10kHz, the response of the aluminium tweeter is approximately 0.8dB higher than the rigid tweeter whereas the diamond tweeter's response differs by only 0.1dB. At 20kHz, the difference is increased to approximately 4.6dB for the aluminium tweeter but is less than 0.5dB for the diamond tweeter.
Regarding figures AI.6 & AI.7 (Structural Acceleration):Note: this flatness of acceleration response is really what should be quoted in specifications; it indicates a purity in real performance which is not obscured by acoustic effects such as phase roll-off. A flat acoustic frequency response can only be achieved by utilizing break-up.
Though the phase responses are similar to 15kHz, the magnitude responses for the two tweeters show a far greater difference (approximately 0.5dB at 10kHz and 3dB at 20kHz) and differences are evident from approximately 10kHz. As the simulations show in figure AI.5, we expect the output of the diamond tweeter to be lower than the aluminium tweeter though care must be taken as here we are comparing an acoustic simulation with a structural measurement.
In the end, the response due to speed of sound in the material used is not necessarily what allows for shallower dome shapes and improved response, it's but one factor of several, including structural rigidity. It was enlightening to learn that flat and extended response is based largely on utilizing breakup. A perfectly rigid tweeter would, in fact, exhibit a somewhat early roll off. This would probably require a phase shield, but for exactly the opposite reason they are used now. It would be used to raise the output at the top end rather than attenuate it as needed now for hard dome breakup peaks.